Stage3D各种投影矩阵的推导

本文将对Stage3D提供的10个投影矩阵逐个推导一遍，能力有限，如有错误请猛喷。

前期准备

我的推导原理是基于下边几个教程的，这些是我搜遍全网找到的最好的教程，只不过大都是OpenGL的，而我这里要基于他们的原理推导一遍Stage3D和WebGL的（下一篇再写WebGL的）。

深入探索透视投影变换深入探索透视投影变换(续)

最详细的矩阵投影3部曲：

1. Perspective Projection Matrix 2. OpenGL Perspective Projection Matrix 3. Orthographic Projection

OpenGL 投影矩阵详细推导过程：

OpenGL Projection Matrix

我只写推导过程，不会详细解释原理，因为原理实在太难说清楚了，不过上边这些教程解释的非常清楚，你可能需要先看一遍再来看我的推导。如果不看，至少要知道这些：

左右手坐标系
透视投影和正交投影是什么
相似三角形
矩阵乘法
线性插值
其次坐标转普通坐标
NDC（Normalized Device Coordinates）

观察Stage3D投影矩阵

先观察一下Stage3D的PerspectiveMatrix3D类提供的投影矩阵。

左手：

perspectiveOffCenterLH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)
perspectiveLH(width:Number, height:Number, zNear:Number, zFar:Number)
perspectiveFieldOfViewLH(fieldOfViewY:Number, aspectRatio:Number, zNear:Number, zFar:Number)
orthoOffCenterLH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)
orthoLH(width:Number,height:Number,zNear:Number,zFar:Number)

右手：

perspectiveOffCenterRH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)
perspectiveRH(width:Number, height:Number, zNear:Number, zFar:Number)
perspectiveFieldOfViewRH(fieldOfViewY:Number, aspectRatio:Number, zNear:Number, zFar:Number)
orthoOffCenterRH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)
orthoRH(width:Number,height:Number,zNear:Number,zFar:Number)

仔细观察后，根据参数不同一共提供了3种透视投影和2种正交投影生成方式，分为左右手两个版本，共10款，总有一款适合你。

提供左右手两个版本说明在眼空间可以任意使用左右手坐标系，只要在最后投影时选择合适的投影矩阵即可。

开始推导

免责声明：不会打公式，全手写，字丑勿怪。

先推导左手坐标系的5个矩阵，函数名和参数太长，眼花了，我来用首字母把参数简写一下。例如： right -> r , width -> w ，zNear -> n , zFar -> f

发现参数都有near和far，区别只在于前几个参数。其实只要推出参数最多的2个典型：

actionscript


1. perspectiveOffCenterLH(left:Number,right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)	
4. orthoOffCenterLH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)

其他的都只是他们的变种而已。从1号典型开始，看最终能否得到官方提供的矩阵：

actionscript

public function perspectiveOffCenterLH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number):void 
{
	this.copyRawDataFrom(Vector.<Number>([
		2.0*zNear/(right-left), 0.0, 0.0, 0.0,
		0.0, -2.0*zNear/(bottom-top), 0.0, 0.0,
		-1.0-2.0*left/(right-left), 1.0+2.0*top/(bottom-top), -zFar/(zNear-zFar), 1.0,
		0.0, 0.0, (zNear*zFar)/(zNear-zFar), 0.0
	]));
}

推导 1. perspectiveOffCenterLH

点p投影到p'，N为近平面，左手坐标系，所以近平面在正z轴方向，画图

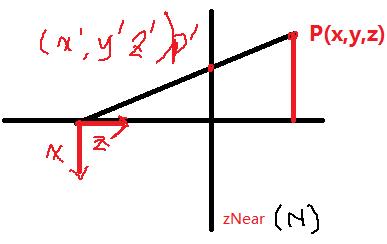
根据大小两个相似三角形，得到

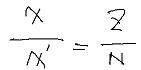
求出x'为

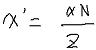
同理 y'为

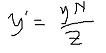
当点P投影到近平面，z'自然永远等于近平面N，所以先不要算他了，后边再说。x' y'已经是投影后的坐标了，但显卡需要的是NDC坐标，所以我们要根据线性插值把x' y'插值到NDC范围内，结果记为xn yn。

注意：Stage3D的NDC范围在(-1,-1,0)到(1,1,1)

已知 left, right,bottom,top ，简写为 l, r, b, t ，投影后的点为x',根据线性插值公式求出缩放后的Xn.

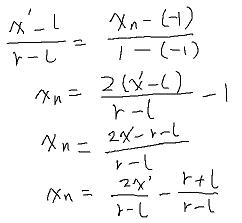
同理yn等于

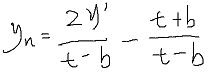
把上边的求得的投影点x',y'带入xn,yn，整理。

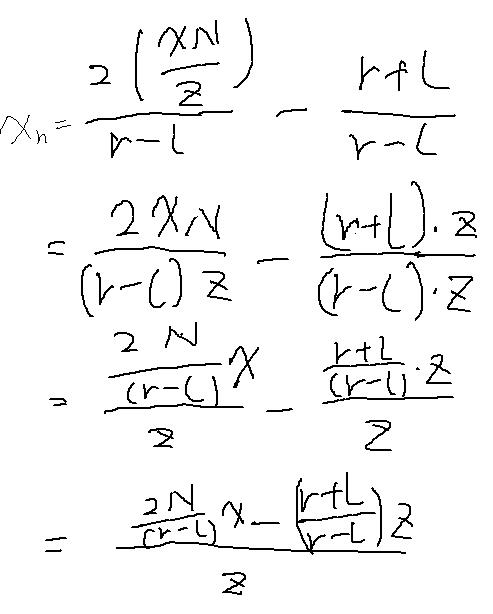
为啥整理成这种形式呢？因为这是一个巧妙的安排，毕竟我们最终要用一个矩阵乘法 + 一个其次坐标转普通坐标 来完成整个转换，把z放到分母可以方便后边做其次坐标转普通坐标，后边会看到两个分子也可以方便的带入矩阵。

同理yn等于

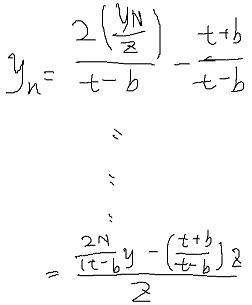
好啦，现在改成矩阵形式，投影前的点**[x,y,z,1]乘以一个矩阵M** 得到的其次坐标，再除以w转成普通坐标后，应该得到的结果为**[xn，yn，zn,1]**求这个矩阵。

注意：Stage3D使用行向量右乘列矩阵

根据上边我们求得的结果，已经可以猜出矩阵部分元素了

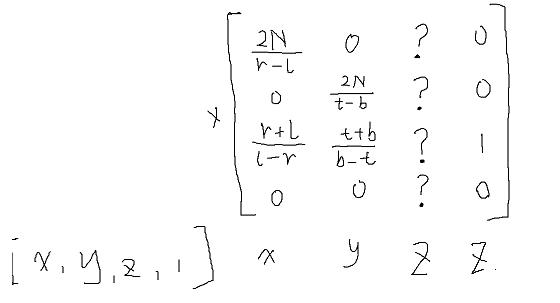
就差z坐标了，z坐标投影后永远等于近平面n，保存他没有意义了，我们要用z来保存转换之前的深度，并线性插值到NDC范围内提供给设备，注意Stage3D中zn的NDC范围在0~1之间，但按照之前xy线性插值的方法，我推不出来 , 需要换种想法了，之前提到的教程里也都是这种方法。

看上边的图，[x,y,z,1]点乘[?,?,?,?] 应该等于转换后的其次坐标z ，由于z与x,y无关，所以把这两个位置都写成0，借助后两个元素A，B来解决线性插值。

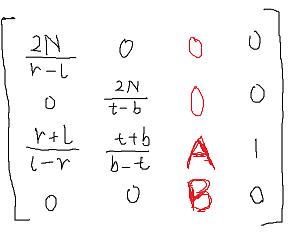
[x,y,z,1] 点乘[?,?,?,?] 就变成了 [x,y,z,1]点乘[0,0,A,B]

zn其次坐标就等于 x * 0 + y * 0 + A * z + 1 * B

其次转普通坐标

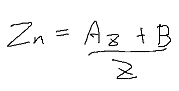
zn的NDC范围在 0~1之间，说明在zNear时为0，zFar时为1，so

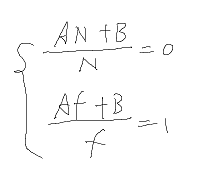
解方程组求A，B

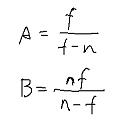
带入矩阵，最终结果

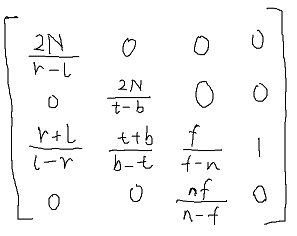
对比一下官方的结果，

actionscript


public function perspectiveOffCenterLH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number):void 
{
	this.copyRawDataFrom(Vector.<Number>([
		2.0*zNear/(right-left), 0.0, 0.0, 0.0,
		0.0, -2.0*zNear/(bottom-top), 0.0, 0.0,
		-1.0-2.0*left/(right-left), 1.0+2.0*top/(bottom-top), -zFar/(zNear-zFar), 1.0,
		0.0, 0.0, (zNear*zFar)/(zNear-zFar), 0.0
	]));
}

好像除了第3行第1列和第2列不一样，其他都一样的。

仔细看看官方给的第3行，第1列

-1.0-2.0*left/(right-left)

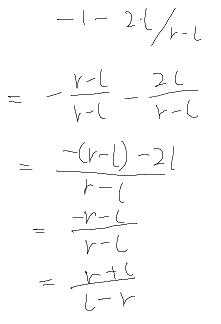
原来跟我们的一样，而且我们的版本更简洁一些：）

第3行第2列也一样，就不写了。

推导 2. perspectiveLH

actionscript


perspectiveLH(width:Number, height:Number, zNear:Number, zFar:Number)

这个是以视口的中心做投影，所以

left = - right top = - bottom

也就是说

r + l = 0 r - l = width

t + b = 0 t - b = height

直接带入上一个推导的矩阵

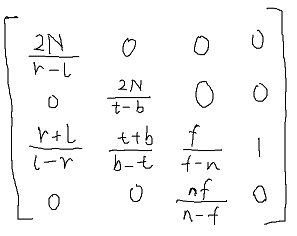
把上边的矩阵简化，得到

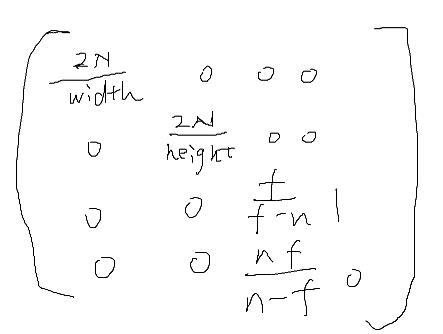
正好是官方的这个，一模一样：

actionscript


public function perspectiveLH(width:Number, height:Number, zNear:Number, zFar:Number):void 
{
	this.copyRawDataFrom(Vector.<Number>([
		2.0*zNear/width, 0.0, 0.0, 0.0,
		0.0, 2.0*zNear/height, 0.0, 0.0,
		0.0, 0.0, zFar/(zFar-zNear), 1.0,
		0.0, 0.0, zNear*zFar/(zNear-zFar), 0.0
	]));
}

推导 3. perspectiveFieldOfViewLH

actionscript


perspectiveFieldOfViewLH(fieldOfViewY:Number,aspectRatio:Number,zNear:Number,zFar:Number)

这里有了两个新参数fov和aspect

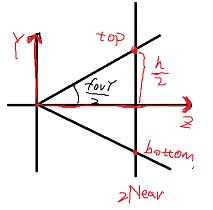
经过研究，这里的 fov 如图所示，是指YZ平面，top和bottom之间的夹角。

看看能不能把这两个参数转成width和height表示，这样就可以直接带入上一个推出的矩阵得到新矩阵了

fov，aspect 与 w ，h是什么关系？

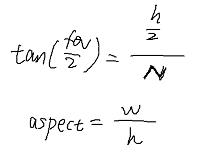
这样就可以把h和w求出来了

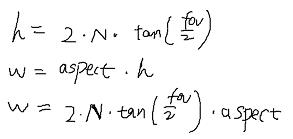
带入上一个矩阵

得到

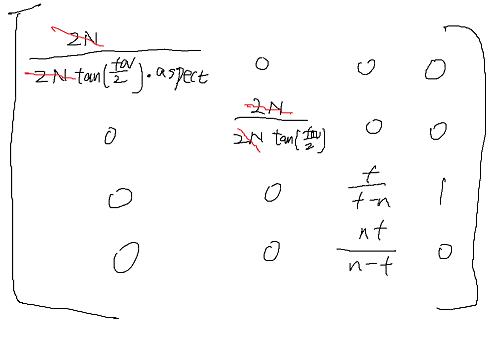
仔细看一下正好与官方提供的一样。

actionscript


public function perspectiveFieldOfViewLH(fieldOfViewY:Number,aspectRatio:Number,zNear:Number,zFar:Number):void {
	var yScale:Number = 1.0/Math.tan(fieldOfViewY/2.0);
	var xScale:Number = yScale / aspectRatio;
	this.copyRawDataFrom(Vector.<Number>([
		xScale, 0.0, 0.0, 0.0,
		0.0, yScale, 0.0, 0.0,
		0.0, 0.0, zFar/(zFar-zNear), 1.0,
		0.0, 0.0, (zNear*zFar)/(zNear-zFar), 0.0
	]));
}

推导 4. orthoOffCenterLH

很难想象这么重要的一个类，官方给的orthoOffCenterLH矩阵居然是错的，而且adobe已经停止支持这个库了，有人提交了错误，也已经没人回应了。

正确的应该是这样的：

actionscript


public function orthoOffCenterLH(left:Number,right:Number, bottom:Number, top:Number, zNear:Number, zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0/(right-left), 0.0, 0.0, 0.0,
		0.0, 2.0/(top-bottom), 0.0, 0.0,
		0.0, 0.0, 1.0/(zFar-zNear), 0.0,
		(left+right)/(left-right), (bottom+top)/(bottom-top), zNear/(zNear-zFar), 1.0
]));
}

推导比透视投影简单，因为是正交投影则，所以

x = x' y = y'

只需要各个方向缩放到NDC范围内就好了，跟之前一样，线性插值

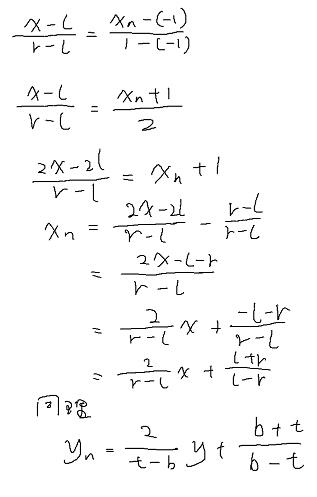
放到矩阵里

Az+B 在近裁剪面为0，远裁剪面为1，so

A n + B = 0 A f + B = 1

解得：

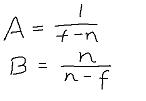
放入矩阵

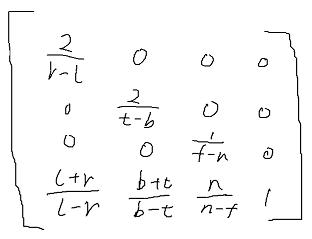
actionscript


public function orthoOffCenterLH(left:Number,right:Number, bottom:Number, top:Number, zNear:Number, zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0/(right-left), 0.0, 0.0, 0.0,
		0.0, 2.0/(top-bottom), 0.0, 0.0,
		0.0, 0.0, 1.0/(zFar-zNear), 0.0,
		(left+right)/(left-right), (bottom+top)/(bottom-top), zNear/(zNear-zFar), 1.0
	]));
}

推导 5. orthoLH

actionscript


orthoLH(width:Number,height:Number,zNear:Number,zFar:Number)

由于是以视口为中心的正交投影矩阵，所以：

left = - right top = - bottom

也就是说

r + l = 0 r - l = width

t + b = 0 t - b = height

带入刚才求得的这个矩阵

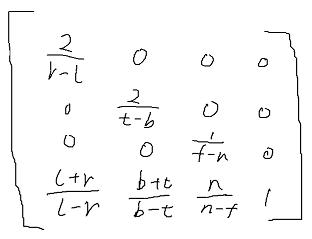
得到：

2/w, 0, 0, 0, 0, 2/h, 0, 0, 0, 0, 1/f-n, 0, 0, 0, n/n-f, 1

对比官方的版本，是一样的

actionscript


public function orthoLH(width:Number,height:Number,zNear:Number,zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0/width, 0.0, 0.0, 0.0,
		0.0, 2.0/height, 0.0, 0.0,
		0.0, 0.0, 1.0/(zFar-zNear), 0.0,
		0.0, 0.0, zNear/(zNear-zFar), 1.0
	]));
}

至此左手5个已经推导完毕，右手的类似，要加快速度了。

推导 6. perspectiveOffCenterRH

从参数最多的开始

actionscript


perspectiveOffCenterRH(left:Number, right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)

点p投影到p' ，N为近平面，右手坐标系，所以近平面在负z轴方向，这次换个方向画图吧

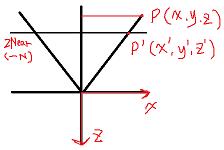
先求投影点x' y',然后插值到NDC范围-1~1之间，结果记为xn yn。

分母都是-z 说明在做透视除法时w为-z ，所以猜到矩阵为

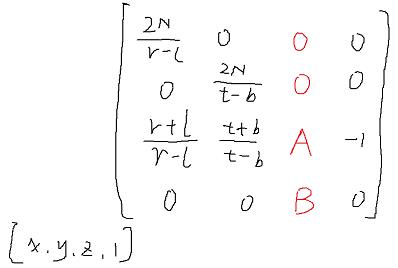
处理z

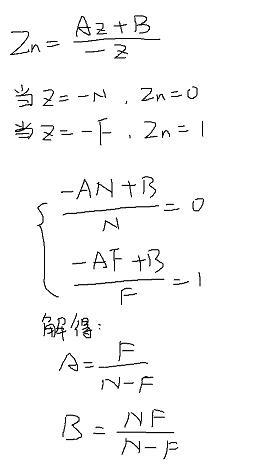
AB带入矩阵

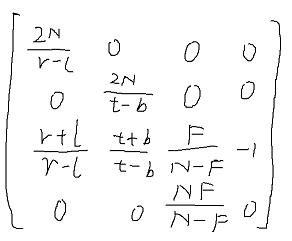
对比官方提供的，稍微整理一下正负号就一模一样了。

actionscript


public function perspectiveOffCenterRH(left:Number,right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0*zNear/(right-left), 0.0, 0.0, 0.0,
		0.0, -2.0*zNear/(bottom-top), 0.0, 0.0,
		1.0+2.0*left/(right-left), -1.0-2.0*top/(bottom-top), zFar/(zNear-zFar), -1.0,
		0.0, 0.0, (zNear*zFar)/(zNear-zFar), 0.0
	]));
}

有了这个，后边两个变种就容易了

推导 7. perspectiveRH

actionscript


perspectiveRH(width:Number,height:Number,zNear:Number,zFar:Number)

以视口的中心做投影，所以

left = - right top = - bottom

也就是说

r + l = 0 r - l = width t + b = 0 t - b = height

直接带入上一个推导的矩阵，得到的结果跟官方一模一样。

actionscript


public function perspectiveRH(width:Number,height:Number,zNear:Number,zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
	    2.0*zNear/width, 0.0, 0.0, 0.0,
	    0.0, 2.0*zNear/height, 0.0, 0.0,
	    0.0, 0.0, zFar/(zNear-zFar), -1.0,
	    0.0, 0.0, zNear*zFar/(zNear-zFar), 0.0
	]));
}

推导 8. perspectiveFieldOfViewRH

actionscript


perspectiveFieldOfViewRH(fieldOfViewY:Number,aspectRatio:Number,zNear:Number,zFar:Number)

跟左手差不多，z轴相反，就不画图了

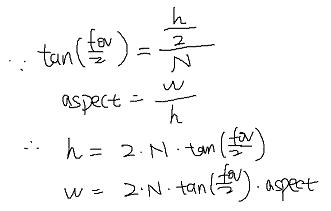
带入上个矩阵

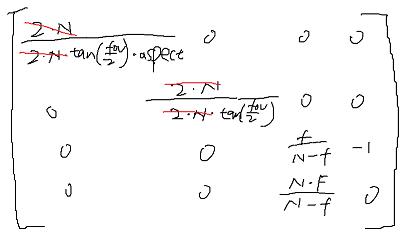
对比，一模一样：）

actionscript


public function perspectiveFieldOfViewRH(fieldOfViewY:Number,aspectRatio:Number,zNear:Number,zFar:Number):void {
	var yScale:Number = 1.0/Math.tan(fieldOfViewY/2.0);
	var xScale:Number = yScale / aspectRatio;
	this.copyRawDataFrom(Vector.<Number>([
		xScale, 0.0, 0.0, 0.0,
		0.0, yScale, 0.0, 0.0,
		0.0, 0.0, zFar/(zNear-zFar), -1.0,
		0.0, 0.0, (zNear*zFar)/(zNear-zFar), 0.0
	]));
}

推导 9. orthoOffCenterRH

actionscript


orthoOffCenterRH(left:Number,right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number)

这个官方提供的矩阵也错了，正确的应该这样：

actionscript


public function orthoOffCenterRH(left:Number,right:Number,bottom:Number,top:Number,zNear:Number, zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0/(right-left), 0.0, 0.0, 0.0,
		0.0, 2.0/(top-bottom), 0.0, 0.0,
		0.0, 0.0, 1.0/(zNear-zFar), 0.0,
		(left+right)/(left-right), (bottom+top)/(bottom-top), zNear/(zNear-zFar), 1.0
	]));
}

因为正交投影，则

x = x' y = y'

直接线性插值到 -1 ~ 1之间

推出矩阵

求变换后的Zn

推导 10. orthoRH

actionscript


orthoRH(width:Number,height:Number,zNear:Number,zFar:Number)

最后一个视口中心投影，这个官方提供的矩阵也有一个笔误 @_@，第3行第3列:

1.0/(zNear-zNear)

应该为

1.0/(zNear-zFar)

开始推导：

r = - l b = -t

r - l = w r + l = 0 t - b = h t + b = 0

带入上边矩阵，很明显得到

actionscript


public function orthoRH(width:Number,height:Number,zNear:Number,zFar:Number):void {
	this.copyRawDataFrom(Vector.<Number>([
		2.0/width, 0.0, 0.0, 0.0,
		0.0, 2.0/height, 0.0, 0.0,
		0.0, 0.0, 1.0/(zNear-zFar), 0.0,
		0.0, 0.0, zNear/(zNear-zFar), 1.0
	]));
}

全文完。